本帖最后由 Miss_love 于 2015-1-6 12:47 编辑
在软件开发的过程中,利用测试的统计数据,估算软件的可靠性,以控制软件的质量是至关重要的。 (1) 推测错误的产生频度 估算错误产生频度的一种方法是估算平均失效等待时间MTTF(Mean Time To Failure)。MTTF估算公式(Shooman模型)是 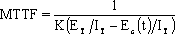 其中,K 是一个经验常数,美国一些统计数字表明,K的典型值是200; ET 是测试之前程序中原有的故障总数; IT 是程序长度(机器指令条数或简单汇编语句条数); t是测试(包括排错)的时间; EC (t) 是在0~t期间内检出并排除的故障总数。 公式的基本假定是: § 单位(程序)长度中的故障数ET∕IT近似为常数,它不因测试与排错而改变。 统计数字表明,通常ET∕IT 值的变化范围在0.5×10-2~2×10-2之间; § 故障检出率正比于程序中残留故障数,而MTTF与程序中残留故障数成正比; § 故障不可能完全检出,但一经检出立即得到改正。 下面对此问题做一分析: 设EC (τ) 是0~τ时间内检出并排除的故障总数,τ是测试时间(月),则在同一段时间0~τ内的单条指令累积规范化排除故障数曲线εc (τ) 为: εc (τ) = EC (τ)∕IT 这条曲线在开始呈递增趋势,然后逐渐和缓,最后趋近于一水平的渐近线ET∕IT。利用公式的基本假定:故障检出率(排错率)正比于程序中残留故障数及残留故障数必须大于零,经过推导得: 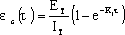 这就是故障累积的S型曲线模型,参看图5.19。 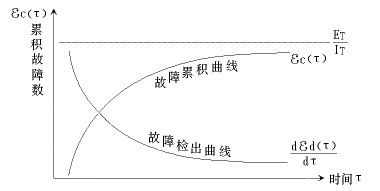 图5.19 故障累积曲线与故障检出曲线 故障检出曲线服从指数分布,亦在图5.19中显示。 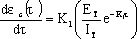 (2) 估算软件中故障总数ET的方法 ①利用Shooman模型估算程序中原来错误总量ET —瞬间估算 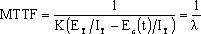 所以, 所以,  若设T是软件总的运行时间,M是软件在这段时间内的故障次数,则 T∕M = 1∕λ= MTTF 现在对程序进行两次不同的互相独立的功能测试,相应检错时间τ1 <τ2,检出的错误数EC (τ1 ) < EC (τ2 ),则有 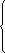 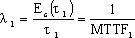 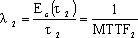 且 且 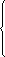 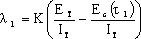 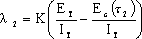 解上述方程组,得到ET的估计值和K的估计值。 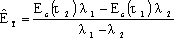 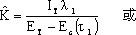 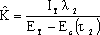 ② 利用植入故障法估算程序中原有故障总数ET ─ 捕获-再捕获抽样法 若设NS是在测试前人为地向程序中植入的故障数(称播种故障),nS是经过一段时间测试后发现的播种故障的数目,nO是在测试中又发现的程序原有故障数。设测试用例发现植入故障和原有故障的能力相同,则程序中原有故障总数ET的估算值为 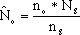 在此方法中要求对播种故障和原有故障同等对待,因此可以由对这些植入的已知故障一无所知的测试专业小组进行测试。 这种对播种故障的捕获─再捕获的抽样方法显然需要消耗许多时间在发现和修改播种故障上,这会影响工程的进度,而且要想使植入的故障有利于精确地推测原有的故障数,如何选择和植入这些播种故障也是一件很困难的事情。为了回避这些难点,就有了下面不必埋设播种故障的方法。 ③ Hyman分别测试法 这是对植入故障法的一种补充。由两个测试员同时互相独立地测试同一程序的两个副本,用t表示测试时间(月),记t = 0时,程序中原有故障总数是B0;t = t1时,测试员甲发现的故障总数是B1;测试员乙发现的故障总数是B2;其中两人发现的相同故障数目是bc;两人发现的不同故障数目是bi。 在大程序测试时,头几个月所发现的错误在总的错误中具有代表性,两个测试员测试的结果应当比较接近,bi不是很大。这时有 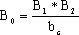 如果bi比较显著,应当每隔一段时间,由两个测试员再进行分别测试,分析测试结果,估算B0。如果bi减小,或几次估算值的结果相差不多,则可用B0作为程序中原有错误总数ET的估算值。
|  /1
/1 
 关于我们
关于我们